利用拼圖遊戲導出商高定理(二)

下列兩圖中，大正方形的邊長都是( a ＋ b )，其中甲是邊長為c的正方形，乙是邊長為a的正方形，丙是邊長為b的正方形，且每一直角三角形的兩股長分別為a、b，斜邊為c：       

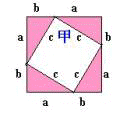
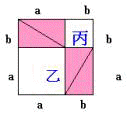
                圖 (一)                         圖 (二) 

 ( 1 ) 上圖(一)中，
甲的面積 ＝ (大正方形面積) － ( 4個直角三角形面積)。

 ( 2 ) 上圖(二)中，
乙和丙的面積和＝(大正方形面積)－( 4個直角三角形面積)。 

( 3 ) 因為圖(一)和圖(二)的面積相等，
所以甲的面積＝乙的面積＋丙的面積

 c²   ＝  a² ＋ b²   ，

即直角三角形的兩股平方和等於斜邊的平方。