|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
窮 竭 法 論 圓 |
|||||
|
阿基米德說 : 給我一個立足點,我就可以移動整個地球 |
|||||
|
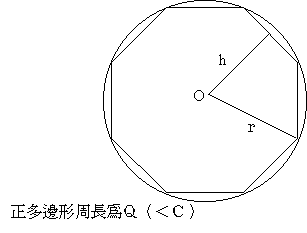
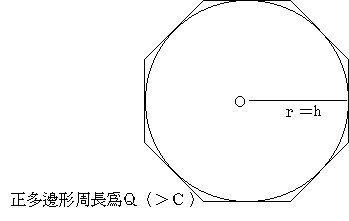
西元前225年左右,阿基米德完成一篇題為《論圓的測量》的短文,它是第一篇深入解析圓面積的論文。 當時的幾何學家已經曉得任何圓形,不論大小,其圓周長度與直徑的比例永遠相同,現代數學家定義π為此常數。然而圓的面積等於什麼呢? 在歐幾里得的《幾何原本》已經證明:兩個圓面積之比與其直徑的平方成正比,但還不知道此比例常數為何?是否與π有關。
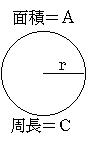
阿基米德命題:圓的面積等於一個以圓半徑為高、圓周長為底之直角三角形的面積 |
 |
|||
 |
|||
|
|
||||||||||||||||||||